Rotational Speed To Linear Speed

Linear Speed Formula (Rotating Object)

Linear Speed Formula (Rotating Object)

The linear speed of a point on a rotating object depends on its distance from the center of rotation. The angular speed is the angle that an object moves through in a sure amount of time. The angular speed has units of radians per 2d (rad/s). There are 2π radians in a full circle. At a distance r from the center of the rotation, a point on the object has a linear speed equal to the angular speed multiplied by the altitude r. The units of linear speed are meters per second, one thousand/south.

linear speed = angular speed x radius of the rotation

v = ωr

v = linear speed (m/s)

ω = angular speed (radians/s)

r = radius of the rotation (m)

Linear Speed Formula (Rotating Object) Questions:

1) A ability drill is on, and spinning at x.0 revolutions per 2nd (rev/s). The diameter of the drill bit is 4.00 mm. What is the linear speed of a betoken on the surface of the drill chip, in meters per second?

Reply: The first step is to find the angular speed of the drill bit. The revolutions per second must be converted to radians per second. There are 2π radians in a full circumvolve.

ω = 10.0 rev/south

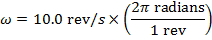
The distance between the heart of rotation and a point on the surface of the drill bit is equal to the radius. The diameter of the drill bit is given, in units of millimeters. The radius in meters is,

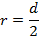
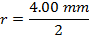
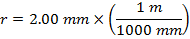
∴r = 0.002 thou

Using the formula v = ωr, the linear speed of a point on the surface of the drill fleck is,

five = ωr

∴5 = (62.8 radians/southward)(0.002 m)

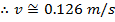
The linear speed of a betoken on the surface of the drill bit is approximately 0.126 m/s. Radians are a "placeholder" unit of measurement, and then they are not included when writing the solved value for linear speed.

ii) Another question.

A sensor is continued inside a car bike, which measures the linear speed. The sensor is 0.080 k from the center of rotation. At that position, the sensor reads that the linear speed of the wheel is 8.00 m/due south. If the radius of the bike is 0.220 g, what is the linear speed on the outer border of the bicycle?

Respond: The linear speed is different at different distances from the center of rotation, but the angular speed is the same everywhere on the wheel. To solve this problem, first find the angular speed using the linear speed at the position of the sensor, 0.080 m. The formula 5 = ωr can be rearranged to solve for the athwart speed ω:

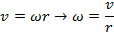
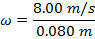
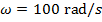
This is likewise the angular speed at the outer edge of the wheel, where the radius is r = 0.220 m. The formula v = ωr can exist used again to solve for the linear speed at that radius:

5 = ωr

v = (100 rad/due south)(0.220 m)

∴v = 22.0 m/s

The linear speed of the auto bicycle at the outer edge is 22.0 m/s.

Rotational Speed To Linear Speed,

Source: https://www.softschools.com/formulas/physics/linear_speed_rotating_object_formula/151/

Posted by: pricewhave1982.blogspot.com

Share this post